Università di Foggia

Dipartimento di Scienze Biomediche

Prof. Crescenzio Gallo

c.gallo@unifg.it

Reti neurali artificiali con Mathematica

Alcune limitazioni

Lezione 9

Premessa

Utilità generali

Disattiviamo i warning

Impostiamo la directory di lavoro

Carichiamo il nostro package delle reti neurali

Introduzione

A questo punto, abbiamo avuto un buon successo con le nostre reti neurali e la loro capacità di riconoscere i modelli complessi. Ancora più impressionante è la loro capacità di generalizzare dal training set per gestire pattern mai visti in precedenza (a parte il fatto che Freud era stato erroneamente classificato ;). Purtroppo, ci sono pattern che hanno un senso intuitivo ma che una rete neurale artificiale non sempre può generalizzare. Daremo uno sguardo in questa sezione.

XOR

Nella Lezione 3 abbiamo discusso il problema dell'XOR:

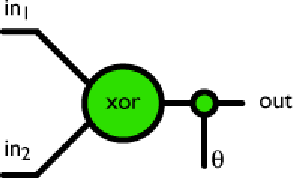
Figura 1. La porta logica XOR.

L'XOR risponde ai suoi input in questo modo:

		out
0	0	0
1	0	1
0	1	1
1	1	0

Tabella 1. La tavola di verità dell'XOR.

Ricordiamo che una rete a singolo strato come quella sopra non era capace di mappare correttamente gli input ai valori di output appropriati per l'XOR. Abbiamo risolto il problema introducendo un altro strato (nascosto):

–

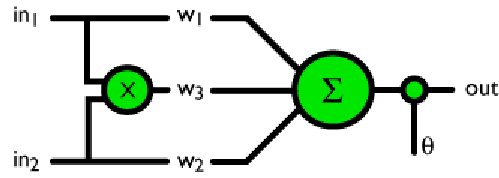
Figura 2. Un neurone artificiale in grado di risolvere il problema XOR.

L'aggiunta di un terzo input, , all'unità di somma ci ha consentito di calcolare correttamente i risultati e risolvere il problema.

Ricordiamo anche che siamo stati in grado di calcolare i pesi ws in modo diretto. Ora che sappiamo qualcosa sull'apprendimento di una rete, possiamo crearne una che può 'imparare' il problema XOR?

La struttura della nostra rete è praticamente già pronta da quanto visto sopra: abbiamo bisogno di due input, un output e apparentemente tre unità nascoste. Così:

Il training set è illustrato in Tabella 1:

Facciamo uso dei parametri di default per il training:

Diamo come al solito un'occhiata ai risultati:

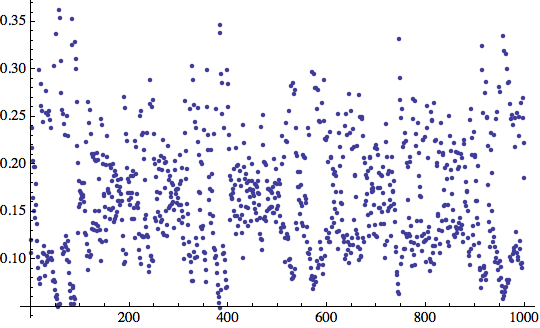
Non sembra molto promettente. L'errore è ancora oscillante dopo

tutte le 1000 iterazioni standard di apprendimento. Come sono i risultati a questo punto?

Pessima rete! Ciascun input produce all'incirca lo stesso, ambiguo, risultato tra 0 e 1. Questo è preoccupante, soprattutto considerando quanto velocemente la rete è stata in grado di apprendere negli altri scenari.

Forse i parametri non sono stati impostati correttamente.

Ripartiamo daccapo:

Aumentiamo l'addestramento portando le iterazioni a 3000 e alzando il tasso di apprendimento η dalla sua impostazione predefinita 0.5 a 0.9. Ricordiamo che i parametri della routine di addestramento trainNN sono i seguenti:

Possiamo riesaminarla per mezzo del comando ? :

Global`trainNN

Eseguiamo il training:

Ora diamo un'occhiata agli errori:

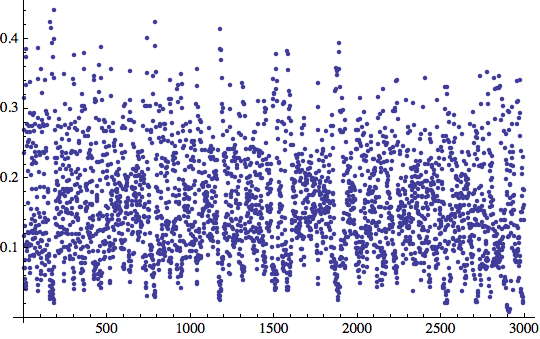
ed ai risultati per il training set:

In qualche modo la rete ha imparato a riconoscere l'input {0,0} ma è ancora confusa sugli altri.

Addestriamola ancora un po' partendo dai pesi ws attuali:

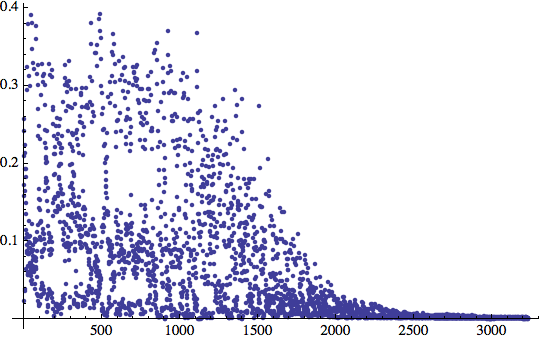
Alla fine sembra che l'errore sia sceso ad un livello accettabile. Quante iterazioni ha eseguito?

Più le iniziali 3000

Sono quindi state necessarie più di 6000 iterazioni per apprendere un tale semplice problema. Per completezza, verifichiamo la nostra tabella di verità:

Da esplorare

Come in precedenza, provare delle versioni con 'runmore' sia nel training che nel testing.

Eseguendo nuovamente l'addestramento potrebbe convergere più rapidamente (o lentamente). Perché?

Possiamo addestrare la rete con una diversa configurazione della matrice dei pesi? Riuscirà ancora ad imparare con appena 2 unità nascoste?

Implementare le altre funzioni logiche di cui abbiamo parlato, cioè l'AND, l'OR ed evemtuali altre. Ci sono funzioni possibili con due ingressi e un'uscita. Implementarle tutte e provare a capire quali sono quelle più facili da addestrare rispetto alle altre.

AND

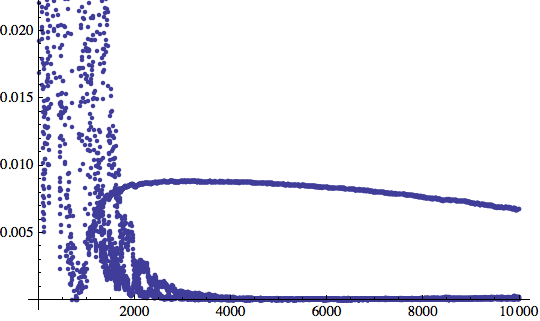
Interessante, vero? Guardiamo la matrice dei pesi e vediamo se è di qualche aiuto:

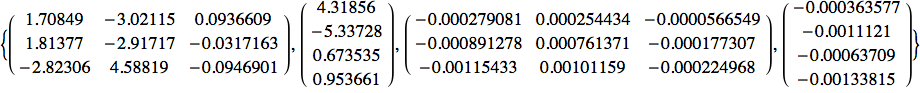
OR

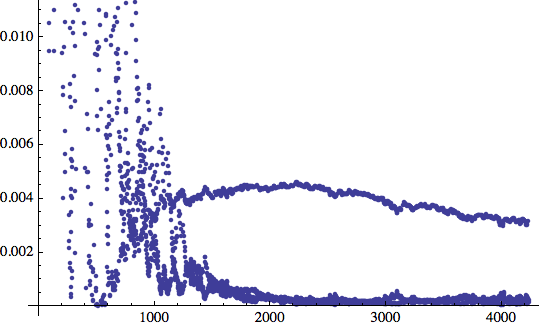
La stessa cosa. Proviamo senza le unità di bias:

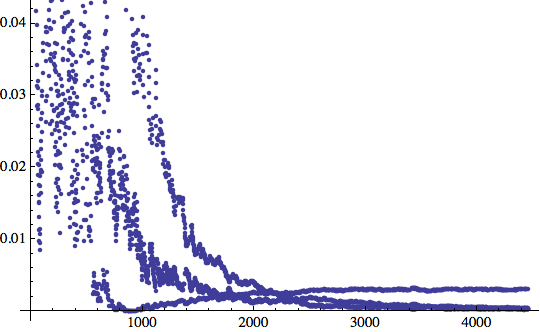
Ahi ahi... Il bias ci stava danneggiando in questo caso!

Che dire della generalizzazione? Si possono insegnare tre di quattro stati e lasciare che la rete intuisca quello mancante?

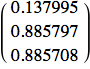
Interessante, ha fatto quello che volevamo, se quello che stavamo facendo era un OR. Ma la risposta non è giusta se volevamo un comportamento come l'XOR.

Proviamo:

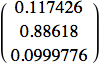
Questa volta ha funzionato... ammesso che fosse ciò che cercavamo (è chiaro il punto?).

Provare ora a modificare il momentum impostando μ a 0.0 e verificare se le cose migliorano.

Infine, è possibile far funzionare le funzioni logiche 'più semplici' (AND, OR) con solo 2 unità nascoste?

Parità

Abbiamo visto che l'apprendimento ha alcune limitazioni, anche con questi semplici problemi.

Un altro problema intuitivamente semplice ma difficile da risolvere è il cosiddetto problema della parità. Molto semplicemente, il problema della parità conta il numero di '1' in un lista binaria (oppure di '0', è la stessa cosa) e dice se c'è n'è un numero 'pari' o 'dispari'.

Così, la lista

ha parità pari, dato che vi sono quattro 1.

Diamo un'occhiata alla tavola di verità dell'XOR e cerchiamo di capire se vi è un modello:

		out
0	0	0
1	0	1
0	1	1
1	1	0

Table 2. Tavola di verità dell'XOR.

Infatti, un output 1 dice che vi è un numero dispari di 1 nella lista d'ingresso, mentre uno 0 indica un numero pari (per i matematici, 0 è pari).

Si vede che il problema della parità è una generalizzazione del problema XOR. E ne eredita tutti i problemi.

Tre

Consideriamo la prima estensione logica, tre ingressi. Ci sono ingressi possibili. Ecco il training set per tutti gli ingressi possibili:

(Si osservi che lo 0 e l'1 dell'esempio XOR qui corrispondono a evenP/oddP)

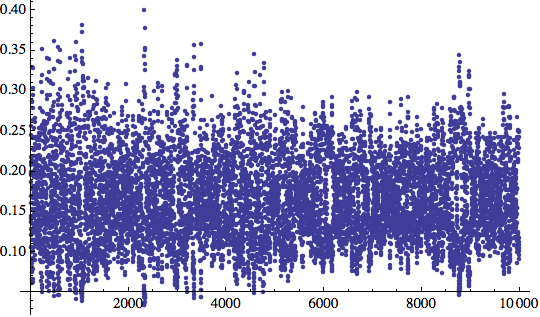
Perbacco! 10000 iterazioni e non ce l'abbiamo ancora fatta.

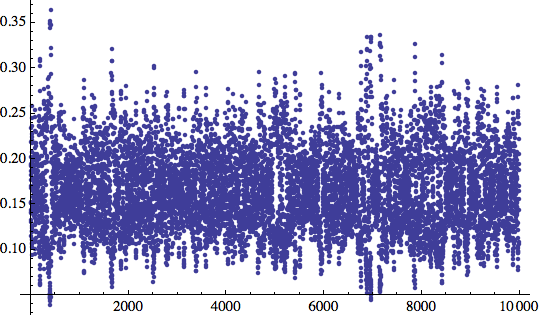
Altre 10000 iterazioni e ancora nessun risultato. Modifichiamo η nuovamente e vediamo se arriviamo da qualche parte:

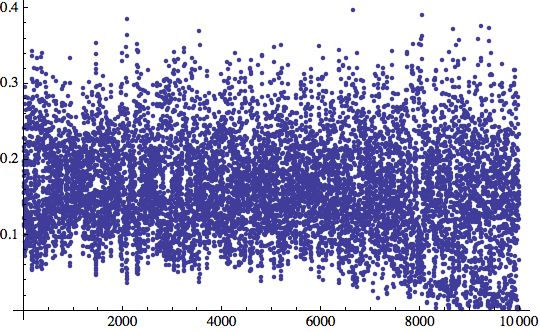
Insistiamo...

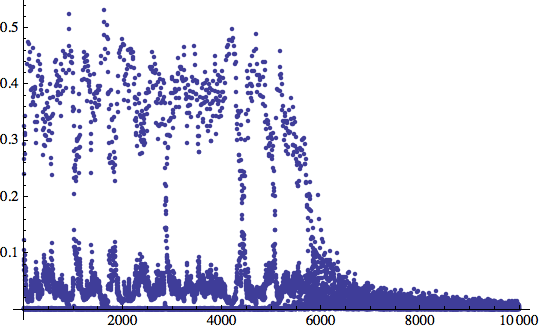
Finalmente sembra che qualcosa si stia muovendo.

Ecco un modo comodo per vedere se gli stati appresi sono gli stessi degli stati di addestramento:

Round[] arrotonda il suo input a 0 o 1 e == controlla se le due liste sono identiche.

Le cose sembrano a posto, ma per quanto riguarda la generalizzazione? Possiamo insegnare ad una rete alcuni prototipi e ricevere successivamente delle risposte adeguate? Questo semplice schema intuitivo è in grado di apprendere?

Da esplorare

Come prima, provare versioni con 'rumore', sia nel training che nel test.

Cosa pensate della funzione soglia Round[]? Riuscite a pensare ad un altro sistema?

C'è qualcosa di Fuzzy in questa tecnica? Esaminare la letteratura della Classificazione Bayesiana per vedere se è possibile perfezionare questo test.

Generalizzare la parità

Consideriamo una lista di lunghezza 20, riempita a caso di 0 e 1

Ecco una semplice funzione che ci dirà la parità di una lista:

E per la nostra lista precedente:

Ecco la configurazione per la nostra rete di controllo di parità

ed alcuni training set casuali (dei 1.048.576 possibili):

Si noti che abbiamo rimappato i valori teorici 0 e 1 sui valori pratici 0.1 e 0.9 come facciamo di solito per mantenere la rete stabile. Inoltre, 'pari' è 0.9 e 'dispari' è 0.1.

Ora eseguiamo l'addestramento:

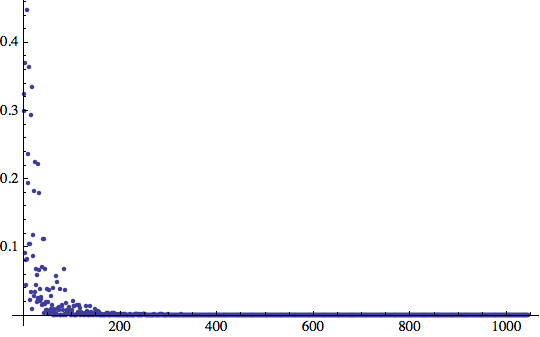
La rete ha subito imparato questo insieme di input (ricordiamo che il criteri di arresto è che l'errore deve scendere al di sotto una certa soglia per almeno il 10% della lunghezza dell'iterazione. In questo caso, avevamo 10.000 iterazioni e la rete converge subito, ma deve continuare per tutta la durata della finestra di training - 1.000 iterazioni = 10% di 10.000).

Infatti, il training set si comporta bene:

Sarà in grado di generalizzare?

Ecco un nuovo insieme di input con i relativi output (corretti):

Qualcosa non ha funzionato...

Ecco le parità vere della lista di cui sopra:

e le previsioni della rete:

Solo 2 su 5 (40%) sono corrette.

Monte Carlo

Facciamo un cosiddetto test di Monte Carlo della rete per vedere quanto sia davvero buona.

Genereremo un gran numero di liste di test, le eseguiremo attraverso la rete e controlleremo le risposte rispetto a quelle corrette. Terremo traccia della percentuale di successo della rete.

Questo calcola la percentuale di successi della rete:

Solo il 70% di successi nel lungo periodo. Questo potrebbe essere tollerabile per alcuni scenari, ma cosa ci vuole per arrivare fino a, diciamo, il 90%?

Abbiamo dimostrato che, con tre ingressi, se addestriamo la rete utilizzando tutti i possibili input può essere corretta al 100%. Purtroppo, con oltre 1 milione di possibili ingressi sarebbe molto più difficile. Con quanti input ce la potremmo fare?

Un maggiore addestramento

Reimpostiamo la rete:

e raddoppiamo il training set (10 righe invece di 5):

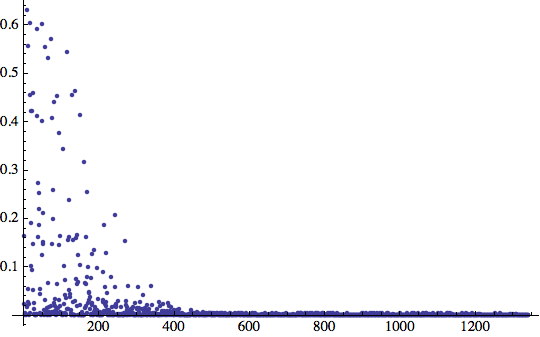
Conserviamola come funzione utile per il futuro:

ed applichiamola al nostro attuale stato dei pesi:

Un attimo! Gli abbiamo dato di più da apprendere eppure ora abbiamo solo il 17% di successi contro il 40%? Che cosa non va?

La risposta sta nella natura del training set. Se entrano gli elementi 'giusti' nel training set la rete avrà più successo. Potrebbe avere appena ricevuto un sacco di stringhe di parità pari e nessun esempio dispari.

Da esplorare

Generalizzare monteCarlo.

Provare con training set sempre più grandi. Riuscite ad immaginare delle regole che aiutino la rete a comportarsi costantemente bene?

Addestramento stocastico

Prima abbiamo identificato un potenziale problema di pertinenza del training set: dal momento che abbiamo più di un milione di possibili input, quali dovremmo usare per addestrare la rete? La risposta in breve è: "Chi lo sa?"

Diamo un'occhiata a un altro modo per addestrare la rete che possa dare molto più successo nel lungo periodo esponendo la rete ad una maggiore variabilità.

Impostiamo la configurazione standard:

Invece di addestrare la rete con lo stessa lista di pattern di input, li genereremo casualmente al volo. Questo assicura che la copertura del possibile spazio degli ingressi sia il più possibile ampio e "imparziale". In teoria, eseguendo il training per qualche milione di iterazioni ogni posizione nello spazio dovrebbe essere esaminata almeno una volta, assicurando che la rete vi abbia almeno dato un'occhiata. Ciò però non garantisce che possa imparare da questo, ma fa almeno in modo che la rete abbia una certa esposizione.

Ecco una routine che genererà una coppia casuale di input/output per la nostra rete:

ed un esempio di esecuzione:

In questo caso, un numero dispari di 1.

Faremo utilizzare al programma di addestramento il generatore casuale invece di una lista predefinita:

Un paio di cose da notare. In primo luogo, il generatore è inserito in una lista (le parentesi graffe {}). Ricordiamo che il nostro algoritmo di addestramento seleziona un elemento casuale dal training set ad ogni iterazione. In questo caso, la lista ha una lunghezza 1, quindi il generatore sarà selezionato di volta in volta.

In secondo luogo, si noti l'assegnazione ritardata utilizzando il :=. Se avessimo usato la normale assegnazione =, la routine generateOne sarebbe stata eseguita immediatamente e il suo risultato sarebbe stato messo nella lista. Il training set ts quindi conterrebbe un valore costante, un solo ingresso possibile. Noi vogliamo un ingresso diverso ogni volta, e questo lo otteniamo grazie all'assegnazione ritardata. Ad esempio:

Come si vede, ogni volta abbiamo per ts un differente training set.

Il che sembrerebbe essere tutto ciò di cui abbiamo bisogno, però abbiamo ancora una cosa da fare:

Perché?

Per lo stesso motivo per il quale abbiamo fatto l'assegnazione ritardata di cui sopra, abbiamo bisogno di ritardare la valutazione del primo parametro di trainNN. Se non facciamo questo, Mathematica  eseguirebbe le seguenti operazioni quando viene richiamata … trainNN[ts,ws,… :

Valuterebbe ciascun parametro, nell'ordine

Fornirebbe i risultati di tale valutazione a trainNN

Nel caso di ws, 10000 e 0.95 questo va bene. Il parametro ws corrisponde alla matrice di stato dei pesi, che è quello che vogliamo: ci limiteremo a leggerla all'inizio e restituirla dopo l'aggiornamento alla fine di tutte le iterazioni. Le costanti (per fortuna) restituiscono il loro stesso valore.

Il problema sorge con ts. Senza l'attributo HoldFirst la routine trainNN valuterà ts prima di passare qualiasi cosa al modulo del programma. Ciò significa che il training set avrà lo stesso valore in tutto il processo di addestramento, proprio come quello che sarebbe successo se avessimo assegnato ts direttamente invece che in modo ritardato.

Con l'attributo HoldFirst, ts viene passato al modulo dell'algoritmo di training senza essere valutato. Sarà perciò valutato solo una volta all'interno del modulo, quando viene usato, cioè durante ogni iterazione di training! Ciò significa che, ad ogni iterazione, trainNN sceglie un elemento casuale dalla lista di training; in questo caso c'è un solo elemento, ts, che quindi viene sempre usato. Poi, assegna le componenti ψ per la propagazione all'indietro (backpropagation) dall'elemento, ts, il che ne provoca la valutazione.

In effetti, anche din=Length[ts[[1,1]]] e dout = Length[ts[[1, 2]]] provocano la valutazione di ts, ognuno però è differente! Questo è qualcosa cui si deve essere attenti se si devono restituire lunghezze diverse, etc. Inoltre provoca anche un po' di inefficienza. Il codice di training dovrebbe essere riscritto per prendere in considerazione questa possibilità. Alla fine,  {ψ,Ψdesired}=chooseRandom[ts] fa sì che la variabile ψ venga caricata e tale valore venga utilizzato in tutto il resto dell'algoritmo.

Ora tutto quello che resta da fare è eseguire l'addestramento. Proveremo con 10000 iterazioni:

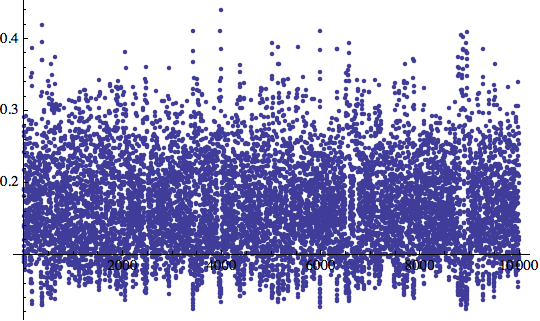
Si noti che l'errore in realtà non scende verso il basso e, in verità, non ce lo aspettavamo: la rete è alimentata di elementi casuali da una lista di 1+ milioni di elementi. Possiamo, però, vedere che l'errore si stabilizza a circa 0.2. Questo è incoraggiante dato il tipo di test che stiamo facendo.

Ricordiamo che prima abbiamo utilizzato Round[] come funzione soglia: i valori superiore a 0.5 erano classificati parità pari, i valori al di sotto di 0.5 come dispari.

Ora che la rete è stata addestrata proviamo un'esecuzione Monte Carlo:

Grande! Abbiamo il 100% di successi!

Da esplorare

Sarebbe interessante realizzare un sistema iterativo in cui si imposta un livello di performance desiderato (ad esempio, in percentuale) e che iteri il training e la sperimentazione avanti e indietro finché non si raggiunge quanto desiderato.

Qual è il minimo addestramento necessario per ottenere, diciamo, una performance del 50%?

Alcuni altri interessanti problemi

Rumelhart e McClelland [2] indicano alcuni altri problemi interessanti con le reti multistrato.

Il problema della codifica (encoding problem)

Cosa succede quando si ha un insieme di input ortogonali (cioè tutti diversi) che si mappano con uscite ortogonali, ma deve passare attraverso un qualche piccolo numero di unità nascoste?

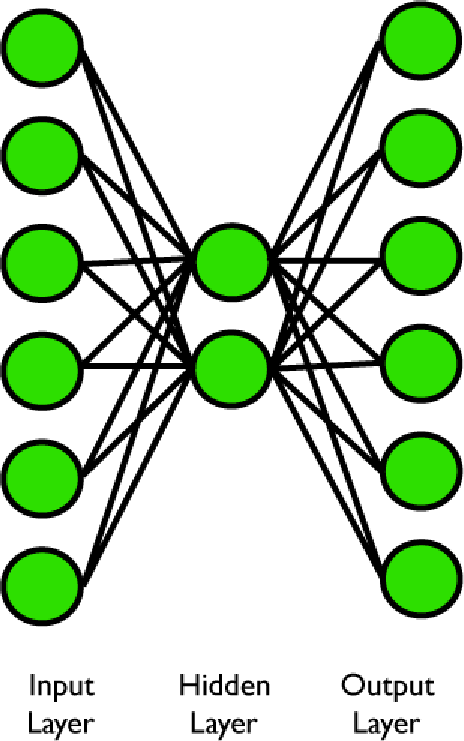
Figura 3. Il problema della codifica.

La figura sopra mostra proprio tale rete. Ackley, Hinton e Sejnowski hanno posto questo problema e, a quanto pare, è trattabile. Il problema generale mappa N ingressi con N uscite attraverso unità nascoste.

Il problema della simmetria

Dato un insieme di input dire se sono simmetrici rispetto agli input centrali.

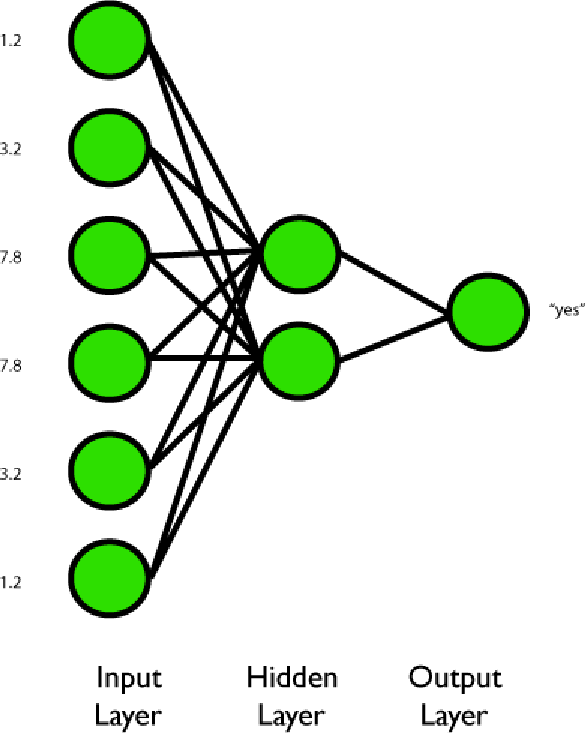
Figura 4. Il problema della simmetria.

Il problema è quello di generalizzare, in modo che la stringa di input:

come pure:

rispondano "sì". Perché è difficile?

L'addizione

Si può insegnare ad una rete ad addizionare numeri binari? Questo significa partizionare la stringa di input in due parti che rappresentano i due addendi. Così all'input

dovrebbe corrispondere l'output

dato che, in binario, Questo è un problema interessante in quanto bisogna tener conto dello schema con cui sono memorizzate le cifre che sono, a tutti gli effetti, separate.

Quando n segmenti (parti) dell'input sono indipendenti/ortogonali si hanno classi di training set per coprire tutte le situazioni possibili. Questo è un problema interessante, in generale, che ora dovremmo avere gli strumenti per affrontare!

Bibliografia

   [1]  Freeman, JA. 1994, Simulating Neural Networks with Mathematica, Addison-Wesley, Reading MA.

   [2]   Rumelhart, DE and McClelland JL, 1988, Parallel Distributed Processing, MIT Press, Cambridge MA.

Created with Wolfram Mathematica 7.0