

Università di Foggia
Dipartimento di Scienze Biomediche
Prof. Crescenzio Gallo

c.gallo@unifg.it
Reti neurali artificiali con Mathematica
Alcuni miglioramenti nell'apprendimento
Lezione 7
Introduzione
Fin qui potrebbe sembrare che le reti neurali siano macchine miracolose: basta insegnare loro e da lì si può generalizzare! Purtroppo, le reti neurali artificiali non sempre convergono su una buona soluzione per un dato problema.
Ci sono alcune tecniche aggiuntive che possono aiutare la nostra rete artificiale lungo il suo percorso per trovare una soluzione; a volte siamo anche in grado di rendere più efficient l'addestramento. È probabilmente importante ricordare qui che i miglioramenti di cui stiamo parlando sono generalmente più utili computazionalmente di quanto non siano concettualmente. Cioè, c'è scarsa correlazione tra alcune di queste aggiunte computazionali e il sistema fisico che tentano di imitare. In alcuni casi (il 'bias' per esempio) si potrebbe fare un po' di analogia con la realtà. Stiamo usando la configurazione fisica del sistema nervoso come una sorta di modello per il calcolo. E' estremamente pericoloso cercare di trarre inferenze causali dai nostri modelli: in sostanza, proprio perché siamo in grado di modellare affidabilmente il comportamento sul computer non significa necessariamente che sia realizzato in quel modo nella realtà.
Ricordiamoci di questo piccolo suggerimento man mano che andiamo avanti.
Bias
Nell'universo delle reti non neurali pensiamo in maniera stereotipata al bias (impulso) come qualcosa di cattivo o da evitare. In realtà il bias, in senso lato, è tutto intorno a noi in varie forme che aiutano a mantenere i circuiti elettrici in funzione, l'acqua a scorrere, e innumerevoli altri sistemi operativi in modo efficiente. Quindi da qui in avanti, pensiamo al nostro particolare bias come una sorta di cosa buona.
Nella nostra rete neurale artificiale possiamo aggiungere bias a ciascun livello del sistema come mostrato qui di seguito:
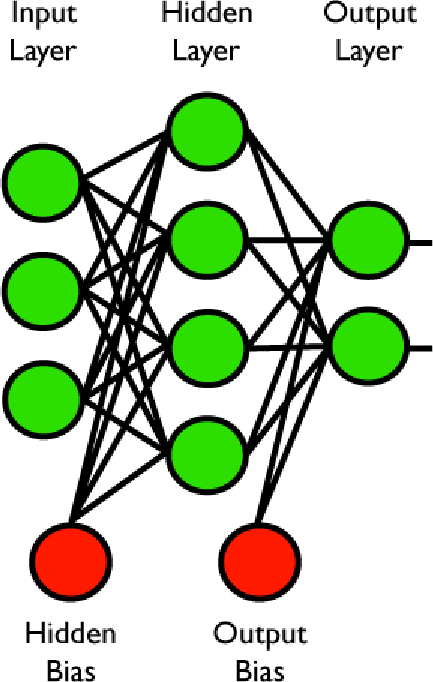
In questo esempio, il bias è un valore costante che viene aggiunto (o sottratto) ad ogni unità dello strato, in modo coerente. Si può pensare l'unità di bias nascosta come un ulteriore livello di unità di input, una unità che non è impostata in modo esplicito. Allo stesso modo, possiamo pensare all'unità bias di uscita come una unità addizionale dello strato nascosto. Anche in questo caso, tuttavia, questa unità non riceve input dalle unità del livello d'ingresso.
Il fatto che il bias di uscita non sia collegato al livello di input ha una implicazione per la tecnica di backpropagation discussa nel paragrafo precedente. In sostanza, poiché non vi è alcun collegamento all'indietro per le unità di bias, non vogliamo che l'errore si propaghi ulteriormente una volta che i loro pesi sono stati adattati.
Implementeremo questo nella nostra rete esistente con un po' di trucchi di programmazione. In pratica, quando propaghiamo le informazioni in avanti (feed forward) nella rete includiamo i pesi, quando andiamo all'indietro (backpropagation) includiamo i bias.
Quindi, quando usiamo i bias aggiungiamo alcuni pesi unitari a ψ e hhidden:

e quando andiamo indietro abbiamo bisogno di rimuoverli (Drop) dal vettore αhidden:
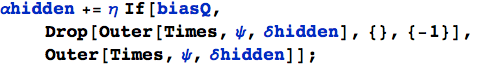
L'effetto dell'aggiunto dei bias è quello di evitare che i pesi non vengano più adattati (ad esempio a causa di un ingresso composto di tutti zeri).
Momentum (quantità di moto)
Un altro utile miglioramento al meccanismo di apprendimento è l'aggiunta del momentum (momento, quantità di moto). Molto semplicemente, il momentum registra la precedente direzione e tasso di variazione per ogni peso e modifica il prossimo aggiornamento del peso di una qualche frazione basata su di esso. L'idea ﹣ proprio come l'inerzia fisica e la quantità di moto ﹣è che, una volta che qualcosa sta andando in una direzione particolare, dovrebbe continuare ad andare in quella direzione fino a quando una forza sufficiente non ne cambia la direzione.
Per programmare questo, aumenteremo un po' i dati sullo stato e terremo traccia del set più recente di correzioni dei pesi degli errori prima del set che stiamo aggiornando. Poi, aggiungeremo una parte di queste correzioni alle correzioni aggiornate. Per esempio:
![]()
dove αoutput è la matrice dei pesi dallo strato nascosto a quello di output nella variabile di stato, e μ è il peso che diamo alla componente momento. Memorizziamo anche αoutputLast nello stato di modo che alla successiva iterazione attraverso la fase di apprendimento possiamo applicarlo al nuovo output, etc. Facciamo la stessa cosa ai pesi dallo strato nascosto a quello di input.
Soglia di errore
Ricordiamo dall'esempio del musicista che abbiamo dovuto 'addestrare' la rete per molte iterazioni prima che l'errore fosse quasi zero. Ma così facendo, si corre anche il rischio di sprecare molto tempo di calcolo ad insegnare alla rete qualcosa che può aver già appreso a qualche iterazione precedente. Per una piccola rete potrebbe non essere un problema, ma per le immagini, dove dobbiamo calcolare matrici di grandi dimensioni, si rischia di perdere del tempo prezioso.
Per ovviare a questo introduciamo il parametro stopε. Se l'errore scende al di sotto di questo valore cesserà il ciclo di apprendimento. Abbiamo comunque bisogno di essere un po' più cauti. L'errore potrebbe scendere al di sotto della soglia per un ingresso di training su una iterazione e poi rimbalzare per un ingresso di training diverso durante l'iterazione di apprendimento successiva. Ciò accade frequentemente nelle prime fasi del processo di apprendimento, e lo possiamo verificare nei grafici di εTable.
Per far fronte a questo introdurremo il concetto di coda di errore εQueue. Questa coda contiene gli ultimi w errori dove n è il numero attuale di iterazioni di apprendimento e 1≤w≤n. Con una struttura a coda, aggiungendo un nuovo elemento alla fine ne esce uno all'inizio. Calcoleremo la media della coda di errore e termineremo l'elaborazione se si è sotto una certa soglia, appunto stopε. Chiameremo w la finestra di errore o εwindow nel codice successivo. Di fatti, calcoleremo la media della finestra, e εwindow è la larghezza di quella finestra.
Nel seguente codice implementeremo il test in questo modo:
![]()
Manterremo l'idea di maxIterations nel codice per impedire che l'esecuzione cicli all'infinito. Cioè, terminiamo se l'errore scende sotto un certo livello accettabile o se abbiamo iterato per un certo numero fisso di iterazioni. Ricordate, possiamo sempre riprendere da dove avevamo lasciato e fare ancora un po' di training in quanto le variabili di stato sono disponibili, memorizzabili e recuperabili.
Altre ottimizzazioni
Nel corso dell'evoluzione delle reti neurali artificiali backpropagation ci sono stati innumerevoli altre ottimizzazioni proposte e attuate dai ricercatori. La Competition between units (concorrenza tra le unità), il Simulated annealing e altre tecniche di ottimizzazione, funzioni di uscita più complicate o specializzate, training set modificati e altri accorgimenti hanno dimostrato di migliorare la convergenza delle reti sul proprio obiettivo di pattern classification.
Programmi modificati
Miglioriamo i programmi sviluppati nell'ultima lezione.
Utilità
Le utilities che abbiamo definito in precedenza sono ancora utili e possiamo continuare ad adoperarle:
![]()

setupNN
Manterremo più o meno la stessa routine setupNN e aggiungeremo un paio di cose per affrontare i bias e il momento come descritto sopra.
La stessa informazione dimensionale è necessaria per la dimensione dell'input, dello strato nascosto e di uscita. Aggiungiamo un ulteriore parametro, bias, per controllare l'aggiunta di unità di bias alle due matrici. Infine, aggiungiamo due matrici per contenere le informazioni sul momentum, cioè lo stato precedente di addestramento delle matrici della rete. Per cominciare le impostiamo a 0 in modo che nessuna informazione sulla 'quantità di moto' venga aggiunta alla prima iterazione.

Diamo un'occhiata allo stato per una rete con 3 unità di input, 2 nascoste ed 1 di uscita:
![]()
La prima matrice di stato è la matrice dei pesi dall'input allo strato nascosto:
![]()
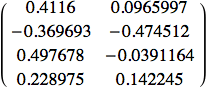
Si noti che ci sono 4 righe di input invece delle 3 specificate. La quarta è l'unità di bias di cui sopra. Stessa cosa vale per la matrice dallo strato nascosto a quello di uscita:
![]()
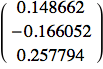
Tre righe invece delle due specificate (anche qui il bias).
Se non vogliamo le unità di bias basta passare il valore False al parametro bias; questo riporta le matrici alle loro naturali dimensioni:
![]()
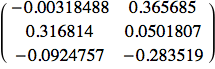
![]()
![]()
Le restanti due matrici sono i valori precedenti di queste due matrici. Si noti che hanno la stessa forma in quanto vogliamo che anche i termini bias persistano nel tempo, se presenti:
![]()

![]()
![]()
trainNN
Abbiamo bisogno di fare alcuni cambiamenti anche al modo in cui il programma di addestramento opera per affrontare i bias e il momentum. La routine completa si trova alla fine di questa sezione. Daremo uno sguardo ad ogni modifica in base al materiale di cui abbiamo parlato sopra. Fare riferimento al codice trainNN completo man mano che si guarda a ogni sezione per vedere come è implementato nella versione finale.
Parametri
Prima di tutto diamo un'occhiata ai parametri della funzione:
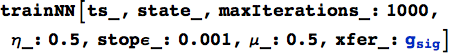
I parametri ts, state, η e maxIterations dovrebbe suonare familiari (anche se abbiamo cambiato nIterations in maxIterations per riflettere il fatto che questo è il limite massimo e non il numero assoluto di iterazioni).
I nuovi parametri sono i seguenti: stopε imposta la soglia di errore per arrestare il processo di addestramento. Una volta che l'errore quadratico medio per le precedenti εwindow iterazioni di training scende al di sotto di questo valore l'addestramento si fermerà. In questa implementazione, calcoliamo εwindow al 10% della lunghezza di maxIterations oppure 10, se superiore. In questo modo otteniamo almeno 10 errori nella nostra media per rendere la finestra efficace. Per disabilitare la verifica della soglia di errore è sufficiente impostare stopε = 0 (o ad un valore negativo se si è realmente intenzionati ad ottenere ogni iterazione).
Il fattore momentum μ determina quanto dello stato di training del passo precedente è aggiunto nello stato corrente. Per disattivare il momentum, basta impostare μ=0 e non verrà utilizzato alcun momentum.
Infine, abbiamo reso la funzione di trasferimento selezionabile tramite il parametro xfer. Di default è impostata la funzione sigmoidea ![]() che abbiamo usato in precedenza. È stata resa flessibile la scelta della funzione di trasferimento in modo da consentire di provare alcune delle altre funzioni descritte in precedenza, come la funzione θ ed altre.
che abbiamo usato in precedenza. È stata resa flessibile la scelta della funzione di trasferimento in modo da consentire di provare alcune delle altre funzioni descritte in precedenza, come la funzione θ ed altre.
Bias
Avrete notato che non vi è alcuna dichiarazione esplicita sulla presenza di unità di bias nelle matrici dei pesi, ma è abbastanza facile da dire guardando le stesse matrici.
Per determinare se ci sono unità di bias basta confrontare la dimensionalità del training set di input con la dimensionalità delle matrici dei pesi. Se c'è un peso in più dell'ingresso, allora abbiamo una unità di bias.

Più avanti nel codice di training faremo riferimento a biasQ (abbreviazione di "bias query") per determinare se vi sono unità di bias presenti.
Ad esempio, quando si sceglie un training set abbiamo bisogno di aggiungere una unità di bias al training set per farlo corrispondere al peso del bias.
![]()
Impostiamo il valore dell'input ad 1.0 perché il peso del bias venga passato inalterato, cioè 1.0 × 'peso del bias'.
Abbiamo anche bisogno di aggiungere unità di bias alle unità nascoste. Questo viene fatto nel modo seguente:
![]()
Infine, abbiamo bisogno di rimuovere queste unità quando salviamo lo stato. La dichiarazione:
![]()
gestisce questo per noi. Non abbiamo bisogno di rimuoverle dall'input ψ in quanto non faremo nient'altro con esso dopo aver eseguito la propagazione in avanti. Nel caso del vettore αtemp abbiamo bisogno di assicurarci che abbia la forma giusta prima di utilizzarlo per la propagazione degli errori.
Momentum
Ci occupiamo del momentum con l'aggiunta di una porzione in scala delle matrici dei pesi precedenti alle nuove matrici dei pesi. L'array di stato diventa:
![]()
Li estraiamo con le istruzioni:
![]()
NB. Avremmo potuto semplicemente scrivere:
![]()
Il fattore di scala μ viene fornito come parametro ed assume il valore di default 0.2 (momentum del 20%).
Quando arriva il momento di calcolare le matrici dei pesi ricordiamo che in precedenza abbiamo fatto quanto segue:
![]()
Abbiamo preso l'attuale αoutput e gli abbiamo aggiunto la correzione degli errori. Per implementare il momentum si calcola il nuovo termine di correzione e si aggiunge il momentum pesato. Memorizziamo questo valore in αoutputLast salvandolo nella variabile di stato per poterlo usare nella successiva iterazione. Poi aggiungiamo la correzione ad αoutput che viene anch'essa salvata nella variabile di stato.
![]()
Mescoliamo il bias e il momentum quando calcoliamo l'errore della matrice dello strato nascosto ed il nuovo valore:
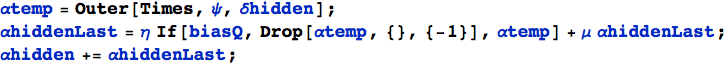
Calcoliamo il termine di errore e lo salviamo in αtemp per evitare di ripeterne il calcolo nell'If (e per ragioni estetiche).
Soglia di errore
Infine, diamo uno sguardo alla realizzazione della soglia di errore. Forniamo il parametro stopε per impostare un criterio di soglia per fermare il training. Ricordiamo che lo facciamo tramite la media di una finestra per evitare che falsi minimi possano inerrompere l'addestramento della rete. Stabiliamo la larghezza della finestra al 10% di maxIterations oppure a 10, se superiore:
![]()
Ora abbiamo bisogno di una coda di errore per conservare gli ultimi εwindow errori. Creeremo εQueue e la pre-caricheremo con valori grandi per evitare che il meccanismo si interrompa fino a quando non viene caricato con valori reali di errore.
![]()
Per mettere un errore (in realtà l'errore quadratico ε.ε) nella coda lo facciamo in due passi. Per prima cosa, rimuoviamo l'ultimo errore tramite Drop[εQueue,-1]. Poi anteponiamo (Prepend) l'errore corrente a tale lista (esamineremo più avanti la dichiarazione Sow; per ora basti dire che restituisce come risultato il suo ingresso). Avremmo potuto utilizzare Append e Drop[...,1], sono entrambi essenzialmente la stessa cosa (memorizzano entrambi la lista in un ordine diverso, ma dato che non importa l'ordine possiamo cavarcela senza).
![]()
Poi controlliamo la media della coda degli errori nel test del ciclo While:
![]()
Il Sow[]…
I lettori più attenti avranno notato l'istruzione Sow[ε.ε], che lavora in collaborazione con l'istruzione εTable = Reap[…] che circonda il ciclo di addestramento While. Ogni volta che Sow[ε.ε] è chiamato non fa altro che 'spingere' il suo valore (in questo caso l'errore quadratico) in una posizione temporanea in cui si accumula con gli argomenti dei precedenti Sow. Quando Reap ('raccolto') viene chiamato, esso restituisce la lista di tutte le cose conservate da Sow ('seminate'). Questo rende la costruzione di elenchi di parti di calcolo più semplice (e lo spazio in realtà più efficiente ed il calcolo più intelligente per quanto riguarda Mathematica).
Qui lo usiamo per costruire la εTable che, come nella precedente 'incarnazione' del nostro trainer, rappresenta la lista degli errori quadratici per ogni sessione di training.
Mettiamo insieme il tutto
Mettendo insieme tutto questo (finalmente!) abbiamo la nuova routine trainNN (il nostro trainer) come illustrato di seguito:

feedForward
Abbiamo bisogno di modificare leggermente feedForward per trattare la nuova informazione di stato, le unità di bias e la capacità di fornire un funzione di trasferimento arbitraria.
![]()
Questo è un modello che corrisponde ad una lista con almeno due elementi, forse più. La tripla sottolineatura dice "corrisponde a qualsiasi cosa e non va assegnato ad alcun nome di variabile". Questi valori sono per i parametri del momentum e sono inutilizzati qui (ricordiamo che il momentum influenza solo il training, ma il bias sia il training che la verifica).
Ci occupiamo del bias allo stesso modo che in trainNN, controllando le dimensioni ed aggiungendo le unità necessarie per convertire i pesi in valori.
Ciò si traduce in:

Testing
Usiamo il problema T-C nuovamente come test. Sappiamo ormai come il tutto dovrebbe funzionare.
T-C test
Ricordiamo dalla Lezione 5 che questa rete, una volta addestrata, è in grado di distinguere tra una 'T' e una 'C'. Per completezza, facciamo in modo che questo funzioni ancora nel nostro ambiente migliorato:

In primo luogo, impostiamo lo stato. Questa rete ha 9 ingressi, 1 uscita e useremo 5 neuroni nascosti come il nostro esempio precedente:
![]()
Questa versione includerà il bias dal momento che non forniamo un valore per il parametro bias.
Ora dobbiamo addestrare la rete. Ricordiamo che forniamo in ingresso il training set ts e il set dei pesi ws. Di default la rete si addestrerà per 1000 iterazioni con η pari a 0.5. Il risultato dell'esecuzione dell'addestramento è una tabella di errori (qui chiamata εTable) e il set finale dei pesi ws.
Per default trainNN utilizzerà una finestra di errore di 100 unità ed un momentum μ di 0.2:
![]()
Ecco un grafico degli errori in funzione del tempo:
![]()
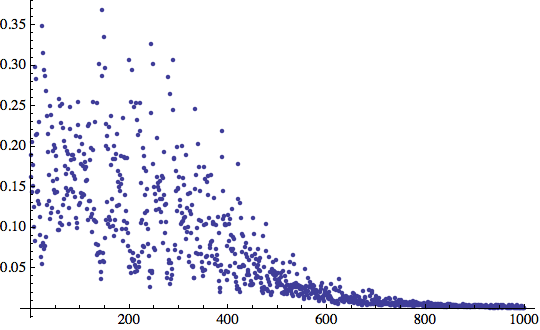
In questo caso
![]()
![]()
la rete ha eseguito tutte le 1000 iterazioni. Modifichiamo leggermente il tasso di apprendimento e il momentum per vedere se può accelerare il processo.
Innanzitutto, resettiamo la matrice dei pesi:
![]()
Ora addestriamo la rete. Andremo con maxIterations pari a 1000, η = 0.8, una soglia di errore di 0.001 e un momentum ('fattore di spinta') di 0.5.
![]()
Quanto tempo ha preso?
![]()
![]()
![]()
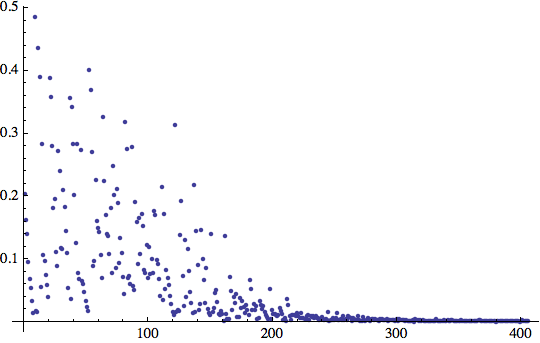
Accidenti! L'errore ha raggiunto il minimo appena dopo circa 200 iterazioni di addestramento.
Verifichiamo gli input. Ricordiamo, 0.9 = T, 0.1 = C. Le prime quattro sono T, le ultime quattro sono C.
![]()

Tutto funziona bene! Abbiamo addestrato la rete in una frazione del tempo usando le modifiche del momentum e del bias e siamo stati abbastanza bravi da fermare il processo di addestramento utilizzando la soglia di errore.
Da esplorare
Provare il problema Sun Ra con questa nuova versione del sistema di apprendimento. Si può fare in modo che impari più efficientemente?
Esplorare i parametri e sperimentare le diverse funzioni di trasferimento. Utilizzando un semplice problema come il T-C capire quanto si può modificare il tasso di apprendimento, il momentum e l'esistenza dei bias. Uno di questi fornisce maggiore aiuto di altri? Sarà così in tutte le circostanze?
Che cosa accade quando si utilizzano le altre funzioni di trasferimento? Si riesce a capire come modificare dinamicamente (da programma) l'inclinazione della sigmoide di base? Cosa succede quando si modifica tale parametro?
Bibliografia
[1] Freeman, JA. 1994, Simulating Neural Networks with Mathematica, Addison-Wesley, Reading MA.
Appendice
Utilità
Disattivo i warning
![]()
General Utilities
Imposto la directory corrente:
![]()