Università di Foggia

Dipartimento di Scienze Biomediche

Prof. Crescenzio Gallo

c.gallo@unifg.it

Reti neurali artificiali con Mathematica

Addestramento e apprendimento

Lezione 5

Introduzione

Fino ad ora, abbiamo avuto a che fare in gran parte con il comportamento di un singolo neurone artificiale. Nell'esempio XOR abbiamo visto una leggera modifica in cui abbiamo aggiunto un bit intermedio (in forma di AND) prima di inviare l'input alla nostra cellula finale, con un conseguente assemblaggio a due neuroni.

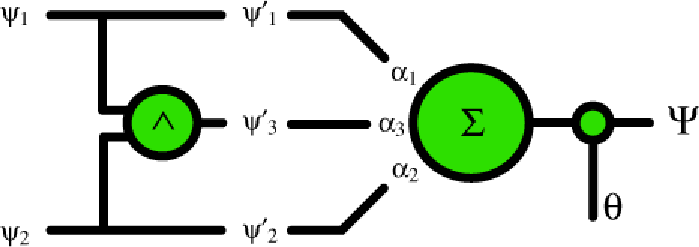
Figura 1. Un XOR. Gli input ψ vengono prima elaborati con un AND (∧). L'output dell'AND, combinato con gli input originari, crea un nuovo vettore di input ψ'. Questo input viene moltiplicato per i pesi α, summato ed infine sottoposto alla funzione soglia per ottenere l'output finale dell'XOR.

A quanto pare, l'unico modo per risolvere il problema XOR, tenuto conto dei vincoli dei neuroni simulati che stiamo usando, è quello di aggiungere ulteriori neuroni artificiali. Un insieme di neuroni si traduce in una rete neurale. In questa lezione studieremo le proprietà delle reti e come possiamo utilizzare insiemi di neuroni artificiali per risolvere problemi molto complicati.

Reti

Una rete (o, più correttamente in questo caso, un grafo) è essenzialmente una collezione di vertici (o nodi) e archi. Nel nostro caso, i nodi rappresentano i neuroni e gli archi rappresentano le connessioni dendriti/assoni tra di essi (sinapsi).

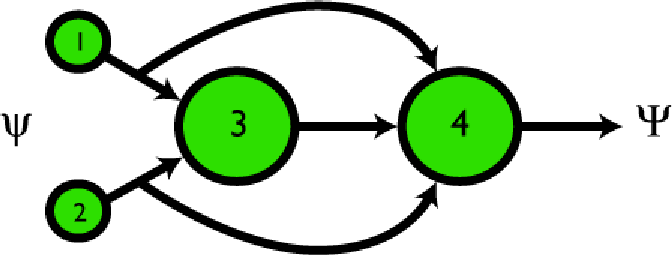
Figura 2. Un diagramma semplificato di rete per il problema XOR. I nodi sono i cerchi verdi, gli archi sono le frecce. I nodi 1 e 2 rappresentano gli input, il nodo 3 l'AND e il nodo 4 rappresenta la sommatoria.

Nella figura sopra si vede un diagramma semplificato di rete per il problema XOR. I nodi (cerchi verdi) e gli archi (frecce) definiscono l'intero sistema.

Mathematica un package molto vasto per la visualizzazione e manipolazione di grafi/reti di molti tipi. È interessante notare che una rete può essere descritta da una semplice collezione di archi. Ad esempio, il grafo sopra può essere specificato tramite la lista ordinata:

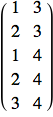
e può essere visualizzato con:

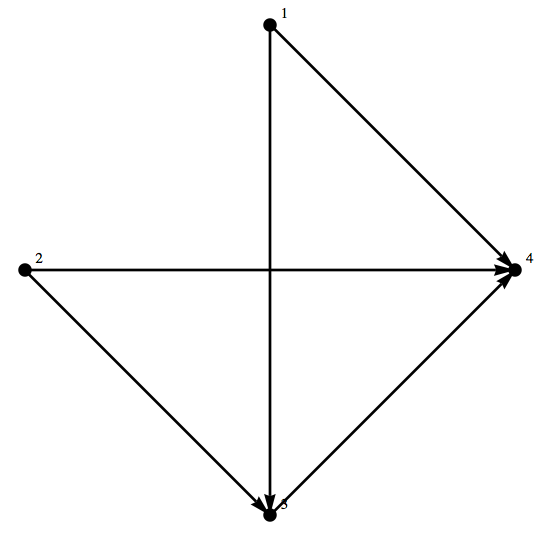
Si può vedere che i nodi 1 e 2 si connettono direttamente al 4 e al 3. Una volta che abbiamo la connettività della rete, come vediamo qui, tutto ciò di cui abbiamo bisogno è un insieme di pesi associati e siamo in grado di simulare una serie di neuroni artificiali interconnessi!

Architettura

L'insieme dei nodi e degli archi di una rete ne costituisce l'architettura. C'è un'architettura particolarmente concisa per le reti neurali artificiali. È meglio pensare ad esse come reti 'a strati' costituite da un strato di ingresso ed uno di uscita combinati con uno o più strati nascosti.

Di seguito è riportato un esempio di una rete con tre ingressi, uno strato nascosto con quattro unità e un livello di uscita finale con una sola unità.

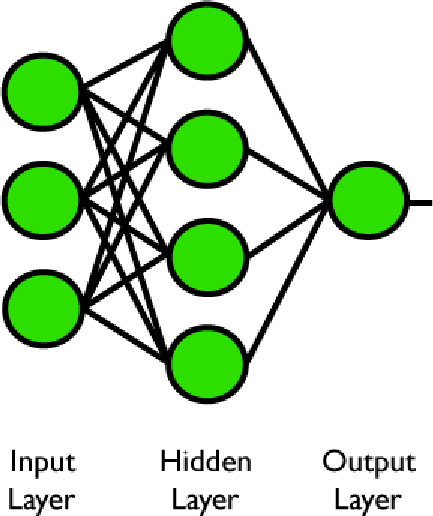
Figura 3. Una rete a tre input e un output con uno strato nascosto. Quest'architettura può essere vista come una che riceve un pattern di input e crea un output binario.

Questo è un tipo di rete che può essere considerata come un sistema che acquisisce un pattern di input e prende una decisione di tipo binario. Per esempio, potremmo volere un sistema che produce un ‘1’ ogni volta che viene attivato un numero dispari di input.

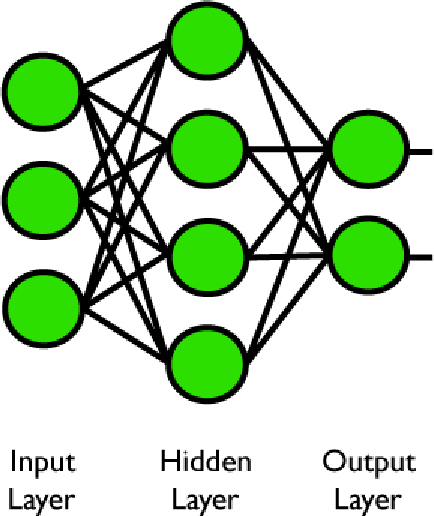
Figura 4. La stessa rete con un output addizionale.

La rete di sopra è progettata per acquisire un pattern di input e produrre un pattern di output. Le reti neurali artificiali sono per la maggior parte di questo tipo. L'obiettivo è, in sostanza, di far corrispondere pattern con altri pattern.

Dato che stiamo parlando di pattern matching, perché non concatenare questi nodi direttamente l'uno con l'altro? Uno riconosce un pattern e ne produce un altro che viene poi immesso in ingresso ad un altro nodo.

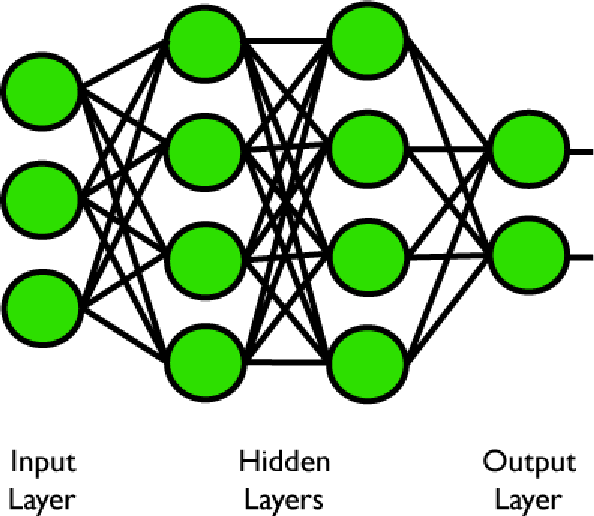
Figura 5. Si può dimostrare che più strati nascosti possono essere consolidati in uno solo.

Sopra abbiamo una rete con più livelli nascosti. I pattern riorganizzati dal primo strato nascosto sono ulteriormente riorganizzati dal secondo prima di essere inviati al livello di output. Si può verificare che, matematicamente, più strati nascosti sono riducibili ad uno solo. Così, una tipica rete neurale artificiale può essere descritta semplicemente come: ingressi, pesi verso il livello nascosto e pesi verso il livello di output.

Come vengono determinati tutti questi pesi?

Backpropagation

Un modo comune per regolare i pesi in una situazione di apprendimento supervisionato è per mezzo di un metodo chiamato backpropagation (retropropagazione). Concettualmente, è abbastanza facile — vedremo alcuni esempi di ingressi e di uscite di rete e regoleremo i pesi con la 'delta rule' discussa in precedenza.

Esploreremo un classico progetto noto come problema "T-C" [1]. L'obiettivo è, come suggerisce il nome, di determinare se una rete ha in ingresso una "T" o "C". Il trucco è che le lettere sono rappresentate in una delle quattro rotazioni possibili, quindi la rete deve lavorare un bel po' per realizzare il suo scopo!

Training set

Questo è il training set del problema. L'input è una stringa di nove valori ‘on’/‘off’ che rappresentano gli stati dei pixel dell'immagine di input. Sono una versione ‘appiattita’ di una matrice di 3×3 pixel. L'output identifica la lettera (T o C).

Il seguente codice Mathematica mostra una rappresentazione grafica degli input da apprendere.

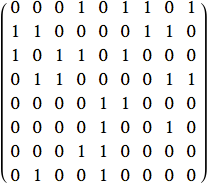
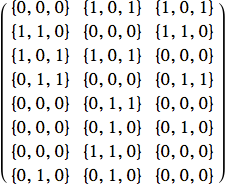
Abbiamo il training set; ora ci occorrono: uno strato nascosto, uno strato di input, un po' di pesi, un tasso di apprendimento (learning rate) e siamo pronti per partire!

Parametri di rete

Per prima cosa definiamo le dimensioni generali della rete. Possiamo ottenere le dimensioni dei vettori di input e di output dal training set: l'input è il primo elemento, l'output desiderato il secondo. Possiamo impostare la dimensione dello strato nascosto arbitrariamente: qui utilizzeremo uno strato nascosto con 5 elementi.

Dimensioni

Abbiamo un input con 9 elementi (una matrice 3×3 'appiattita'), 5 elementi nascosti ed un singolo output (che dirà se è una ‘T’ o una ‘C’).

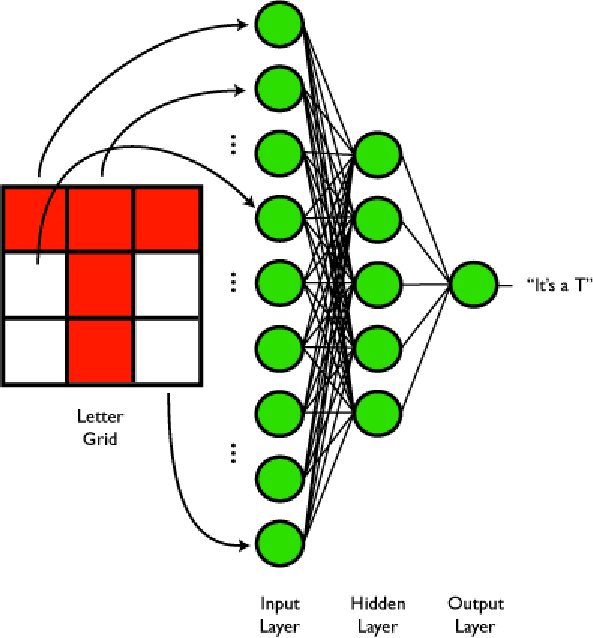
Figura 6. La configurazione della nostra rete. Gli input rappresentano i valori bianco-nero delle 9 celle di una matrice 3×3. Ci sono 5 unità nascoste ed un singolo output la cui decisione discrimina tra le due lettere.

Tasso di apprendimento (learning rate)

Imposteremo il tasso di apprendimento η a 0.1:

Pesi iniziali casuali

Come con l'esempio della regola delta abbiamo bisogno di una collezione di pesi nascosti da regolare. Qui avremo bisogno di due liste bidimensionali che rappresentano i pesi degli ingressi verso il livello nascosto ed i pesi dello strato nascosto verso il livello di output.

In Mathematica possiamo usare il package "Statistics`ContinuousDistributions" e la funzione RandomArray[] per creare in maniera efficiente liste e matrici di numeri casuali secondo qualche distribuzione predefinita.

Definiamo prima una distribuzione dalla quale ricavare i pesi:

Questa definisce una distribuzione uniforme con limiti [-0.5,0.5].  Ora creaiamo i pesi come segue:

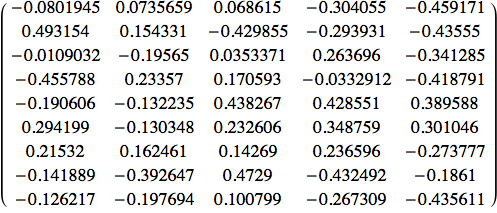
Ciascuna riga rappresenta le connessioni di un input con ciascuno dei neuroni nascosti. Per esempio, la prima entrata è il peso che va dal neurone di input 1 al neurone nascosto 1, la successiva è il peso dall'input 1 al nascosto 2 e così via.

Ora abbiamo bisogno di un array analogo contenente i pesi dalle nostre unità nascoste verso l'unità di output:

Carichiamo i pattern che vogliamo testare

Utilizziamo il comando Mathematica ReplaceAll[] (abbreviato qui nella notazione infissa /. ) per assegnare valori a on, off, isaT, isaC. Possiamo salvarli nella variabile ts per un uso successivo.

I valori scelti per on, off, isaT, isaC sono del tutto arbitrari. L'idea è di avere dei numeri che siano chiaramente differenti l'uno dall'altro per rispettare le condizioni binarie di partenza. Avremmo tranquillamente anche potuto usare 0.88, 0.12 o qualsiasi altra coppia di numeri sufficientemente 'distanti' tra di loro.

C'è un problema sottile se si decide di utilizzare i valori 0 e 1. Ricordate che il processo che stiamo usando si basa sulla moltiplicazione dei pesi. Le moltiplicazioni per 0 e 1 sono casi particolari che portano i valori intermedi della rete ai limiti dei valori che vogliamo trattare, senza lasciare nulla della gamma dinamica di cui abbiamo bisogno per ottenere una rete performante. Ci ritorneremo più avanti.

Propagazione in avanti (forward propagation)

Per cominciare, inseriamo manualmente uno degli input nella rete e vediamo come approssima l'output desiderato. Ricordate, questi pesi sono casuali: quindi, se esiste una corrispondenza perfetta con l'uscita  desiderata sarà un risultato puramente casuale.

Diamo un'occhiata alla prima coppia del training set:

La prima lista è il set di input, la seconda l'output desiderato. Possiamo mapparli nelle due variabili ψ e mediante la seguente assegnazione:

Ora iniziamo il processo di inserimento dell'input nella rete.

Prima mltiplichiamo il vettore di input ψ per la matrice dei pesi dello strato nascosto . Ciò risulterà in un vettore di uscita dallo strato nascosto, che daremo come argomento all'appropriata funzione di trasferimento o di uscita (, la funzione sigmoidea nel nostro caso) e ne utilizzeremo il risultato come input per il passo successivo memorizzandolo in una variabile temporanea :

Ricordiamo che il prodotto scalare ha l'effetto di moltiplicare ogni ingresso con tutti i pesi appropriati, sommandone i risultati.

Ora trasferiamo le uscite dallo strato nascosto attraverso lo strato finale. Memorizzeremo il risultato finale prodotto dalla rete nella variabile , in modo da poter calcolare l'errore alla fine:

contiene invece l'output desiderato; la differenza dà:

il che non è ancora un buon risultato.

Per ricapitolare. Abbiamo alimentato ciascuna delle 9 unità di input, trasferendone i risultati alle 5 unità nascoste, pesato quindi per ed infine inviato l'uscita di ciascuna unità nascosta all'unità di output, pesando per . Quindi abbiamo calcolato l'errore tra il risultato atteso () e quello ottenuto . Comunque questo era solo uno degli input; come si comporterà a rete con i restanti?

Esempi

1.   Proviamo con gli altri input. Come sarà l'errore (abbiamo cambiato leggermente la notazione per non alterare i risultati precedenti)?

2.   Proviamo una distribuzione diversa per generare i pesi casuali.

Un po' meglio...

3.  Proviamo un'altra funzione di output:

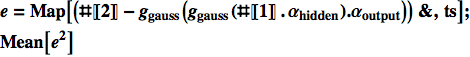
Backward

Vedremo ora l'adeguamento dei pesi attraverso la back-propagation (retropropagazione). Abbiamo fatto funzionare la rete in 'avanti', ottenendo le uscite e gli errori. Ora, usando la regola delta abbiamo bisogno di correggere i pesi per avvicinare il risultato un po' più a quello desiderato.

Secondo la regola delta vista nell'ultima sezione, il δ complessivo per l'output è:

Il δ per lo strato nascosto è un po' più complicato. Essenzialmente, in questo caso abbiamo una serie di errori il cui δ è stato appena determinato nel passaggio precedente.
Per ottenere l'errore di rete degli strati nascosti dobbiamo eseguire il prodotto scalare tra il appena ottenuto e i pesi dello strato di output (matematicamente parlando, abbiamo bisogno di trasporre la matrice dei pesi perchè il prodotto scalare funzioni correttamente):

Il completo è perciò:

Adesso abbiamo i nostri due δ da applicare ai rispettivi α. Ricordiamo che nella regola delta si aggiunge una frazione del δ ai pesi, cioè:

α = α + η δ

Adattare i pesi in questo caso è un po' più complicato. Ora abbiamo un insieme multidimensionale di pesi, ed è quindi necessario applicare appropriatamente il δ ai vari input. Utilizzeremo allo scopo la funzione  Outer[] che calcola il prodotto esterno generalizzato di due liste. Ad esempio:

Il prodotto esterno generalizzato consiste sostanzialmente in tutte le possibili combinazioni di ciascuna lista, passate come parametri alla funzione specificata, ad esempio la moltiplicazione Times[]:

In sostanza, abbiamo bisogno di fare il prodotto esterno del delta degli output nascosti e quello finale per adattare i pesi delle unità di output finali. Ricordiamo che l'output dello strato nascosto è:

ed il δ appena calcolato è:

Ora dobbiamo aggiornare . Faremo uso del tasso di apprendimento η per ridurre in scala l'adattamento dei pesi, come nella sezione precedente.

Inoltre abbiamo bisogno di 'scalare' anche i pesi . Facciamo il prodotto esterno tra il δ nascosto e l'input:

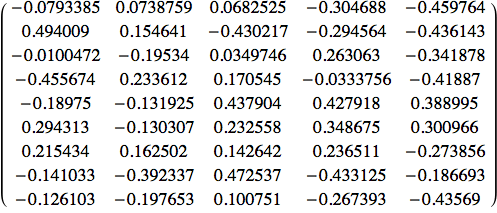
Abbiamo appena eseguito un passo dell'algoritmo di apprendimento, regolando gli α per gli strati nascosti e di uscita. Ricordiamo però che lo abbiamo fatto su un solo ingresso, il primo (la T normale). Proviamo ora ad inviare tutti gli input alla rete per vedere che tipo di previsioni ci darà.

Ecco una semplice funzione che accetta un input e lo trasferisce attraverso la rete. Ora abbiamo bisogno di moltiplicare gli ingressi per i pesi nascosti e le uscite nascoste per i pesi di output. In un'unica elaborazione:

Per mappare tutti gli input attraverso la rete, possiamo fare uso della funzione Map[] (/@) ottenendo i risultati:

ts[[All,1]] è la lista contenente tutti i primi elementi (gli input) del training set. I risultati per ora sembrano un po' indistinti. In realtà, sembrano abbastanza omogenei (ricordiamo che dovremmo avere 0.9 per una 'T' e 0.1 per una 'C'). Questo non è davvero sorprendente, dal momento che abbiamo eseguito solo una sessione di training sugli α (ricordiamo che in precedenza sono occorse centinaia di iterazioni per ottenere qualcosa di ragionevole).

Visto che ci siamo, perchè non calcolare l'errore, l'errore quadratico e la media degli errori quadratici?

L'errore quadratico medio è:

L'errore può essere calcolato in una sola riga:

Training automatizzato

Abbiamo chiaramente bisogno di automatizzare il processo di training (o apprendimento supervisionato). Per questo adotteremo la seguente strategia:

Selezionare un elemento a caso dal training set

Propagarlo in avanti (forward) nella rete (cioè la funzione eseguiPrevisione[] di prima)

Calcolare gli errori e i δ

Adattare gli α

Ripetere finché l'errore è al di sopra di una qualche soglia o per un numero massimo di iterazioni

Il seguente blocco di codice realizza il tutto (iterando alcune centinaia di volte) e genera una tabella degli errori (si osservi che ε.ε dà l'errore quadratico):

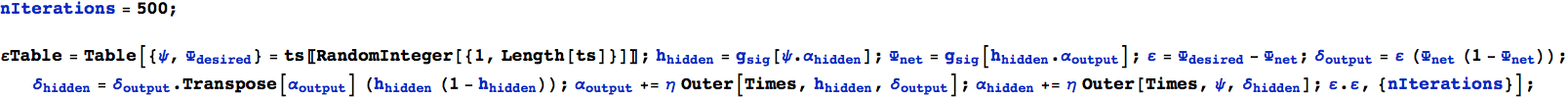
Per le prime 500 iterazioni otteniamo i seguenti errori:

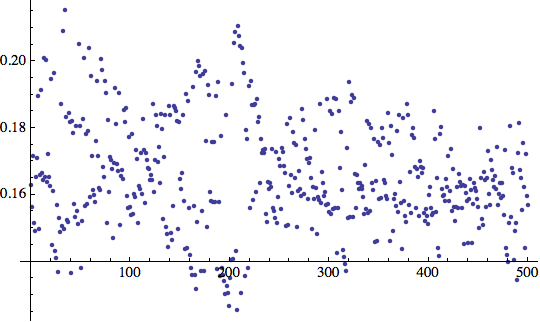
Perchè gli errori appaiono così sparpagliati?

Ricordiamo che il training set consiste di due tipi di input/output: una 'T' e una 'C'. Inizialmente, i pesi casuali non hanno alcuna possibilità di distinguere tra i due tipi di risultati e, quindi, produrranno grosso modo lo stesso output in entrambi i casi.
L'errore sarà perciò al di sopra o al di sotto di questo numero a seconda se sia una T (cui abbiamo assegnato il valore 0.9) o una C (con valore 0.1).
È interessante osservare come l'errore oscilla man mano che la risposta corretta viene individuata.

Ancora!

Dopo queste 500 iterazioni possiamo osservare glio output che otterremmo se fornissimo in ingresso gli input del training set alla rete:

Ricordiamo da sopra che i primi quattro input sono delle T e dovrebbero avere un'uscita 0.9 mentre gli altri quattro input dovrebbero essere delle C con 0.1, ma non si vede ancora una netta separazione. Eseguiamo ancora alcune migliaia di iterazioni e osserviamo gli errori (utilizzeremo Join[] per appendere la lista attuale alla lista degli errori esistente):

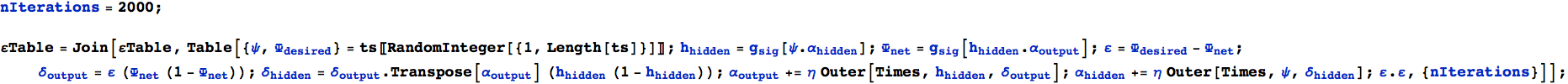
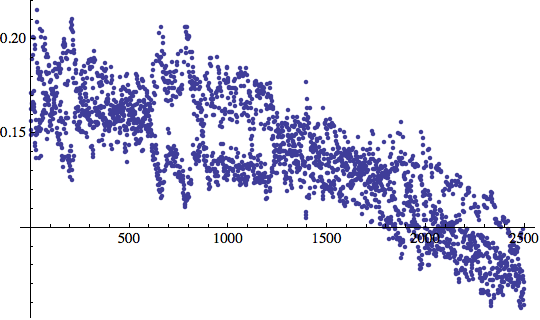
Otteniamo un risultato più accettabile:

Si vede che l'errore prende forma, anche se non si è ancora del tutto stabilizzato:

Allora eseguiamo qualche ulteriore iterazione:

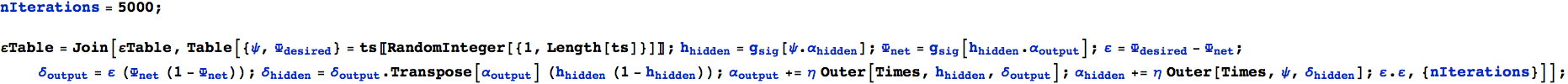
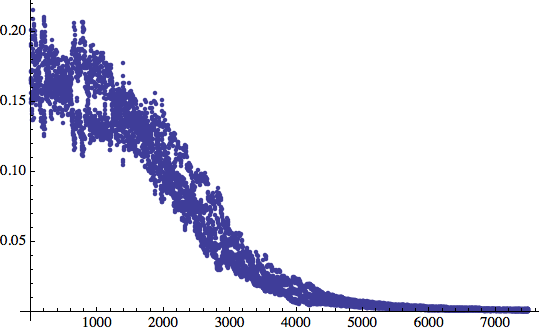
Ora le cose vanno molto meglio. Ogni volta che inseriamo un ingresso di tipo T nella rete, otteniamo un output 0.9, mentre quando inseriamo una C otteniamo 0.1. Congratulazioni! Abbiamo appena addestrato la nostra prima rete neurale artificiale!

Abbiamo visto che le iterazioni sono state eseguite per tentativi: c'è un modo sistematico per portare a termine l'addestramento?

La migliore strategia è quella di calcolare l'errore quadratico medio ad ogni iterazione. Quando l'errore raggiunge un minimo il processo termina. Possiamo fare questo controllo alla fine di ciascuna iterazione:

e fermarci quando il valore raggiunge un qualche limite predefinito.

Un po' di rumore

Abbiamo quindi addestrato la nostra rete. Sembra che risponda bene al training set; ad esempio:

Ma cosa succede se forniamo in ingresso una lettera leggermente distorta? Diamo un'occhiata ad una T incompleta:

Diamola in ingresso alla nostra rete:

Quindi la T è correttamente classificata! Si tratta di un risultato alquanto impressionante, se si pensa che la rete, addestrata con pochi esempi, è stata in grado di fare una previsione generale anche con un input che non aveva mai osservato prima!

Questa è una delle cose realmente potenti che le reti neurali artificiali possono fare: generalizzare. Nelle lezioni successive trarremo vantaggio da questa capacità ed impareremo alcuni altri meccanismi di apprendimento insieme al modo per rendere le reti ancora più flessibili e adattabili.

Esempio

   Proviamo un insieme differente di lettere 'disturbate'.

Nessun rumore:

Un po' di rumore:

Molto:

Niente male!

Bibliografia

   [1]  Freeman, JA. 1994, Simulating Neural Networks with Mathematica, Addison-Wesley, Reading MA.

Appendice

Utilità

Disattivo i warnings

Package utilizzato per la distribuzione normale

Funzioni di trasferimento

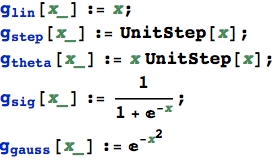
Distribuzioni statistiche

Created with Wolfram Mathematica 7.0