Università di Foggia
Dipartimento di Scienze Biomediche
Prof. Crescenzio Gallo
c.gallo@unifg.it
Reti neurali artificiali con Mathematica
Il Perceptron
Lezione 2
Introduzione
Il nostro interesse è qui principalmente rivolto nell'attività di elaborazione di informazioni effettuata da diversi (e talvolta moltissimi) neuroni interconnessi.
Dal punto di vista puramente computazionale possiamo tranquillamente ignorare il processo (elettrochimico) che fa attivare un neurone, e piuttosto concentrarci sul semplice risultato di tale attivazione e di come essa possa comunicare informazione.
Il Perceptron
Verso la fine degli anni '50 - inizio degli anni '60 Rosenblatt propose svariate macchine che gettarono le basi per l'avvento delle reti neurali artificiali. Tali macchine erano chiamate Perceptrons (percettroni) ed erano basate sul lavoro (1940) di McCulloch e Pitts sul calcolo logico di meccanismi neurali. [1,2,3]
Le macchine di Rosenblat erano collezioni di unità come quelle mostrate nella figura sotto. Per questo motivo, il nome perceptron è stato utilizzato per denotare non solo le macchine ma (più comunemente) le unità di elaborazione stesse. Variazioni di queste unità prendono il nome di ADALINE, Sigma-node, etc.
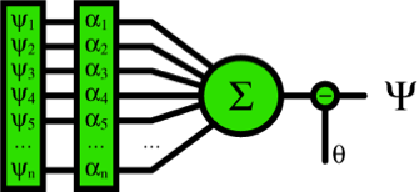
Figura 1. Un perceptron base. Gli input 
sono moltiplicati per i rispettivi pesi 
. Tali input pesati vengono addizionati e, se il valore risultante eccede una qualche soglia θ, l'output Ψ 'scatta' (solitamente rappresentato con un ‘1’). Altrimenti l'output è assente (situazione di solito rappresentata con uno ‘0’).
Il perceptron è un analogo del neurone biologico descritto in precedenza. In sintesi, il perceptron è un neurone artificiale che elabora l'informazione proveniente da diversi ingressi (input) e, per mezzo di una qualche regola decisionale, attiva o meno la sua uscita (output). Gli input corrispondono ai dentriti e l'output rappresenta l'assone di un neurone biologico. Un complesso di tali unità connetterà gli output (assoni) di alcune cellule agli input di altre, creando una struttura virtuale o artificiale.
In breve, il perceptron raccoglie diversi input, li pesa, li addiziona e quindi prende una decisione se attivarsi o meno in base a tale somma pesata.
Tipicamente gli input sono binari — cioè valgono 0 o 1: tali valori rappresentano rispettivamente l'assenza o la presenza di attività. Infatti, i neuroni biologici si comportano in gran parte in questo modo.
Non c'è distinzione tra "quantità" di attivazione, solo la sua presenza o assenza. Dal momento che l'uscita di un percettrone è binaria ne consegue che anche l'ingresso verso altre cellule sarà binario. I pesi agiscono per condizionare questi ingressi, sottolineando alcuni e de-enfatizzandone altri prima che vengano sommati. Dopo questa sommatoria viene presa la decisione se attivare o meno l'uscita. Il tipo più semplice di decisione è la cosiddetta decisione a soglia. Prenderemo in esame diversi tipi di funzioni di decisione nelle sezioni successive.
Notazione
Utilizzeremo la lettera greca minuscola ψ per indicare un input, tipicamente un vettore di n componenti: in tal modo, 
indicherà la terza componente di input.
I pesi verranno indicati con la lettera greca minuscola α, con 
che anche qui indica il "terzo" peso. La sommatoria viene indicata con Σ, mentre con θ verrà indicata la funzione di attivazione.
Lo stato finale del neurone (acceso o spento) è un valore binario rappresentato dalla lettera greca maiuscola Ψ.
Sintetizzando
| (1) |
dove θ rappresenta di solito la Heaviside unit step function (funzione a gradino).
La Somma
Iniziamo esaminando il processo della sommatoria degli input.
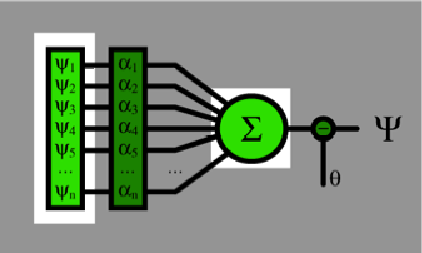
Figura 2. Gli input e la loro sommatoria.
Rappresentiamo in Mathematica il vettore degli input con una lista.
Nell'esempio sopra abbiamo un (vettore di) input di dimensione 5. Il primo e gli ultimi due input provengono da neuroni attivati, mentre il secondo e il terzo sono inattivi.
Possiamo sommare i valori della lista usando questa notazione:
dove l'operatore Plus si dice che è applicato alla lista (le due '@' denotano l'applicazione, un'abbreviazione per la funzione Mathematica Apply[]) e vediamo il relativo risultato, 3. Semplificando potremmo dire che, per un perceptron a 5 ingressi, se 3 o più input sono attivi allora il perceptron si attiverà anch'esso.
Ciò può essere sufficiente ma non consente alcuna sorta di regolazione dettagliata degli ingressi, in sostanza non consente di dire che alcuni input sono “più importanti” di altri.
Somma pesata
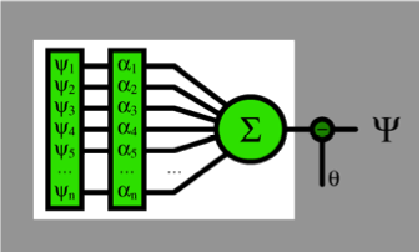
Figura 3. Pesare gli input e sommarli.
Ecco l’input ψ con il relativo set di pesi α:
Moltiplicando il vettore di input per il vettore dei pesi
si ottiene un nuovo insieme di valori, il vettore di attivazione. Sommiamolo come abbiamo fatto prima:
Questo valore finale (talvolta indicato con h) è chiamato valore di attivazione o attivazione netta del perceptron.
Naturalmente avremmo potuto ottenere immediatamente il valore di attivazione semplicemente facendo il prodotto scalare (interno) del vettore di input per il vettore dei pesi (in Mathematica si utilizza l’operatore ‘dot’):
Osserviamo che il risultato della sommatoria non è sempre binario, ma può essere un qualunque valore reale.
Somma pesata con soglia
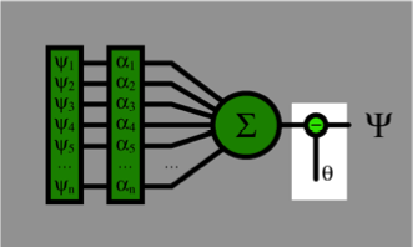
Figura 4. Aggiunta della funzione soglia.
In una rete neurale, sia fisica che artificiale, le uscite dei neuroni (assoni) servono come input per altri neuroni (sinapsi). Per ora abbiamo deciso di vincolarci ad un perceptron con uscita binaria (si attiva o no, 1 oppure 0). In questo esempio abbiamo un valore netto di attivazione di h = 4.3, ma abbiamo bisogno di convertirlo in uno dei due stati di cui sopra, 0 o 1.
La funzione UnitStep[] di Mathematica restituisce 0 se il suo input è inferiore a zero, 1 altrimenti (è quindi un’implementazione della Heaviside unit step function). Possiamo perciò usarla come semplice funzione di decisione: se la somma degli input pesati è maggiore o uguale a zero allora il perceptron si ‘attiva’ (cioè produce il valore 1 in uscita, verso i neuroni collegati a valle), altrimenti no.
Ripetendo il processo della somma degli input pesati:
e quindi applicando la funzione soglia UnitStep otteniamo l’uscta finale del perceptron:
Si vede che, per il dato input ψ ed i pesi α il nostro perceptron si attiva!
La funzione soglia, indicata con θ(x) come nell’equazione 1, opera nel seguente modo:
| (2) |
Una notazione più generale per la funzione di uscita è g(x), come illustrato nella prossima sezione. In tal caso la specifica funzione soglia è indicata con 
.
Funzioni di attivazione (uscita o trasformazione)
Sappiamo che in una rete neurale (fisica o artificiale) gli output dei neuroni (assoni) servono da input agli altri neuroni (sinapsi). In una rete con uscita binaria (0 o 1) vi è la necessità di convertire il valore di attivazione h nell’informazione binaria di attivazione (1) o meno (0) del neurone. Ad esempio, se abbiamo h=-3.1 dobbiamo convertire questo valore in uno dei due valori binari.
Questa trasformazione è ottenuta utilizzando una funzione di uscita (anche chiamata funzione di trasformazione o di attivazione) genericamente indicata con g(x).
Funzione a gradino (Step Function)
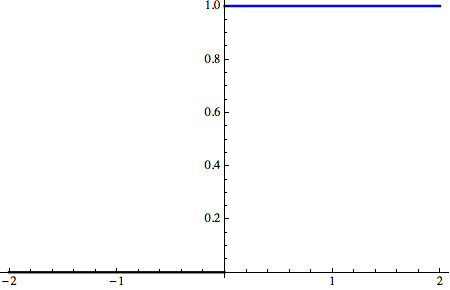
Abbiamo già esaminato la semplice funzione a gradino (unit step) θ(x), anche indicata con 
:
| (3) |
In Mathematica, le funzioni sono indicate (nella forma di input normale InputForm) con:
Utilizzando la forma tradizionale (TraditionalForm) in Mathematica, si ottiene una rappresentazione matematicamente più chiara:
Si ricordi che la funzione a gradino opera nel seguente modo:
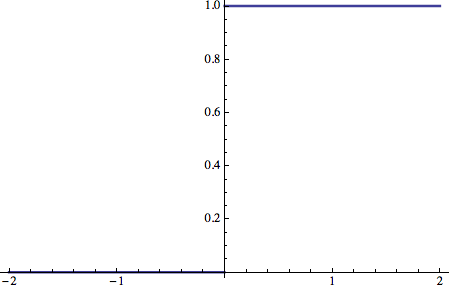
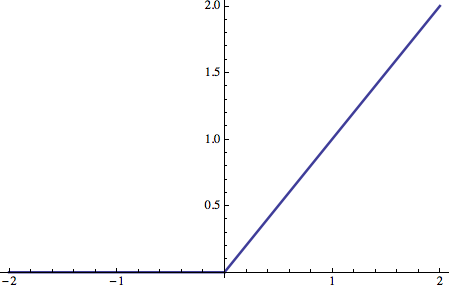
Funzione lineare (Linear Function)
Una funzione di attivazione frequentemente utilizzata è il semplice trasferimento lineare:
| (4) |
In Mathematica:
e graficamente:
Funzione θ (Theta Function)
Vi è una funzione usata meno frequentemente chiamata 
che non è la funzione a gradino UnitStep bensì la sua versione modificata:
| (5) |
Il risultato è una funzione lineare, ma solo quando x>0.
In Mathematica:
e graficamente:
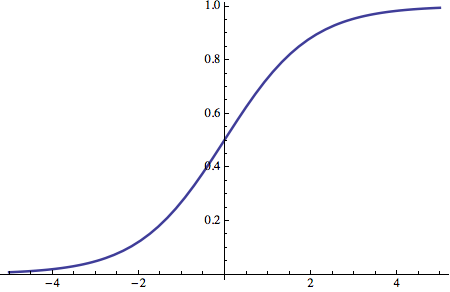
Funzione sigmoidea (Sigmoid Function)
La funzione sigmoidea è una funzione di attivazione comunemente usata nelle reti neurali artificiali. Matematicamente:
| (6) |
e graficamente:
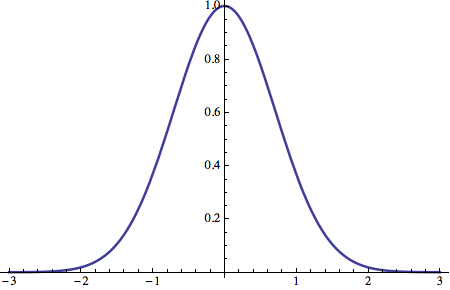
Funzione gaussiana (Gaussian Function)
Un’altra funzione interessante dal punto di vista statistico è la funzione di attivazione gaussiana:
| (7) |
Graficamente:
References
[1] McCulloch, WS, Pitts, W. 1943, 'A logical calculus of the ideas immanent in nervous activity', Bulletin of Mathematical Biophysics, vol. 5, pp 115–133.
[2] Rosenblatt, F. 1959, ‘Two theorems of statistical separability in the perceptrton’, Proceedings of a Symposium on the Mechanization of Thought Processes, Her Majesty's Stationary Office, London, pp. 421–456.
[3] Rosenblatt, F. 1962, Principles of Neurodynamics, Spartan Books, New York.
